Fabio A. González, Raúl Ramos-Pollán & Joseph Gallego
Quantum Machine Intelligence, Volume 7, Article 94 (2025)
Published: 07 October 2025
DOI: 10.1007/s42484-025-00299-9

Abstract:
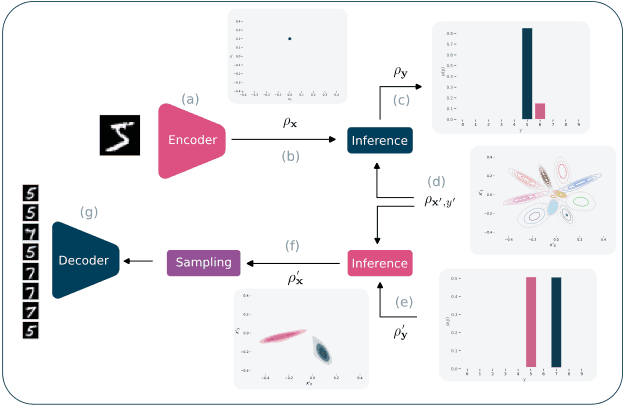
This paper introduces a novel approach to probabilistic deep learning, kernel density matrices, which provide a simpler yet effective mechanism for representing joint probability distributions of both continuous and discrete random variables. In quantum mechanics, a density matrix is the most general way to describe the state of a quantum system. This work extends the concept of density matrices by allowing them to be defined in a reproducing kernel Hilbert space. This abstraction allows the construction of differentiable models for density estimation, inference, and sampling, and enables their integration into end-to-end deep neural models. In doing so, we provide a versatile representation of marginal and joint probability distributions that allows us to develop a differentiable, compositional, and reversible inference procedure that covers a wide range of machine learning tasks, including density estimation, discriminative learning, and generative modeling. The broad applicability of the framework is illustrated by two examples: an image classification model that can be naturally transformed into a conditional generative model, and a model for learning with label proportions that demonstrates the framework’s ability to deal with uncertainty in the training samples. The framework is implemented as a library and is available at: https://github.com/fagonzalezo/kdm.

Keywords: Quantum machine learning • Density matrix • Kernel methods • Probabilistic deep learning

Links:

• 📄 Publisher page
• 📑 Download PDF (Springer)
• 💻 GitHub implementation (as referenced in article)

📌 BibTeX citation

@article{gonzalez2025kernel,
  title   = {Kernel density matrices for probabilistic deep learning},
  author  = {Gonz{\'a}lez, Fabio A. and Ramos-Poll{\'a}n, Ra{\'u}l and Gallego, Joseph},
  journal = {Quantum Machine Intelligence},
  volume  = {7},
  pages   = {94},
  year    = {2025},
  doi     = {10.1007/s42484-025-00299-9}
}